Jump to:
Reading Braille
There are several challenges when reading braille that math teachers should be aware of.
Braille characters have limited variation, making them difficult to distinguish from one another. This issue becomes particularly evident when reading dense mathematical text, like equations, which often lacks contextual cues. Another challenge is that braille readers may mirror or reverse characters during reading, often due to spatial perception difficulties.
It is important to pay close attention to the braille reading, since accurately decoding the characters and symbols is crucial for understanding and performing mathematics. If needed, consult with a professional to improve the student’s braille reading skills. When students use a laptop with a braille display, combining speech synthesis with tactile reading may help reduce errors. Ensure that all numbers, symbols, operators and letters are vocalized while using speech synthesis. Braille readers should select the highest verbosity setting (“all”).
Reading Strategies
Getting an overview of an equation is often a quick process for sighted students. For a braille reader, it can take more time. To support braille readers in comprehending an equation, you can use this step-by-step instruction:
- Read or listen to the equation.
- Give a verbal description of the equation using mathematical vocabulary.
- Find the equal sign.
- Examine the left-hand side of the equation. What kind of expression is this? What is the structure? Are there any powers, roots, or parentheses?
- Examine the right-hand side of the equation. What kind of expression is this? What is the structure? Are there any powers, roots, or parentheses?
- Determine the first step needed to solve the equation.
- Begin solving the equation.
To ensure that the braille reader uses correct mathematical vocabulary, it is important to facilitate communication between the braille reader, the math teacher, and classmates. For instance, “x^2” should be articulated as “x squared”, rather than “x circumflex two”.
Verbal Description
Braille readers may benefit from a verbal description of an equation, as it prepares them to understand the equation’s structure. When working with braille reading students, it is important to provide verbal descriptions of visual elements that sighted students might take for granted, such as the positioning of terms (left or right of the equal sign), and how parentheses are used. Take the following equation as an example:
![]()
A verbal description could be:
“This is an equation with one unknown, x. The equation has three terms: two on the left side of the equal sign and one on the right. All the terms consist of a fraction multiplied by a parenthesis.”
The Writing Process
Sighted students are able to use lines, drawings and color-coded steps to show their equation solving process. Braille readers need to use other strategies since they work digitally, and the notation is linear. As a result, the intermediate steps in their work may differ from those of sighted students. It’s important for you, as a math teacher, to discuss with the braille reader which intermediate steps to include and how best to represent them.
As an example, let us look at the equation 5(x + 3) ‐ 4 = 10. A sighted student might solve the equation like this:
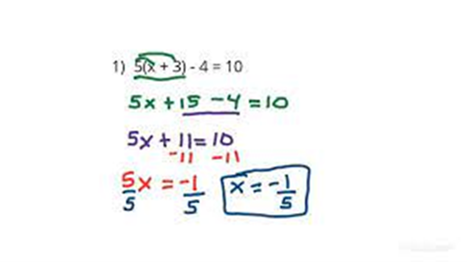
A braille reader might solve the equation like this:
5(x + 3) ‐ 4 = 10
5x + 15 ‐ 4 = 10
5x + 11 = 10
5x + 11 = 10 ‐ ‐11
5x = -1
5x = -1 //5
x = -1/5===
Note that two spaces followed by two operation symbols indicates that the operation is performed on both sides of the equal sign. The final answer is marked with “===”.
As a starting point, it can be beneficial to provide some worked examples in braille on paper, as this can give a more comprehensive understanding of what a solution entails. The advantage of using braille on paper is that it offers a better overall view.
We will give you examples of how an equality and an inequality may be solved linearly.
Example 1
1/2(x + 2) ‐ 1/3(x ‐ 1) = 1/3(1/2 + 4x)
x/2 + 1 ‐ x/3 + 1/3 = 1/6 + 4x/3
x/2 + 1 ‐ x/3 + 1/3 = 1/6 + 4x/3 **6
3x + 6 ‐ 2x + 2 = 1 + 8x
x + 8 = 1 + 8x ‐ ‐8x ‐ ‐8
-7x = -7 //-7
x = 1===
In this example, the equation is copied and pasted on the line below, before continuing with the calculations.
Example 2
x(x + 3)(x ‐ 2) >= 0
To solve the inequality, we can use sign lines for each factor in the expression on the left-hand side. While it is important to align the lines below each other for sighted students, this is of no use for the braille reader.
When writing sign lines, use the signs for addition (+) and subtraction (-) if they are easy to discriminate in the braille notation used. If not, use “,” for negative values and “:” for positive values. Make one line for each factor, like this:
x(x + 3)(x ‐ 2) >= 0
x ,,,0:::
x + 3 ,,,-3:::
x ‐ 2 ,,,2:::
x(x + 3)(x ‐ 2) ,,,-3:::0,,,2:::
Solution: x(x + 3)(x ‐ 2) >= 0 when -3 <= x <= 0 and when x >= 2.
Inequalities may also be solved using a table showing the sign of the factors for different intervals of x, like this:
| x | x + 3 | x ‐ 2 | x(x + 3)(x ‐ 2) | |
| x < -3 | ‐ | ‐ | ‐ | ‐ |
| -3 < x < 0 | ‐ | + | ‐ | + |
| 0 < x < 2 | + | + | ‐ | ‐ |
| x > 2 | + | + | + | + |
The table shows that the expression x(x + 3)(x ‐ 2) is positive or zero when -3 <= x <= 0 and when x >= 2.
For more detailed information about the strategies for solving equations, see the instructional guide on equations for ICT-professionals.
For details on how to solve equations tactile graphs, see the instructional guide on equations for tactile image reading professionals.
