Jump to:
Digital Equation Solving
Before a braille reader starts using a digital tool to solve equations, make sure the tool is accessible to them and that they know how to use it. The more proficient braille readers are with the digital tools, the better they can focus on mathematics.
CAS (Computer Algebra System) software is part of the mathematics curriculum in many countries. CAS allows students to work with both simple and advanced algebraic expressions and equations. The most commonly used CAS program in schools is GeoGebra. GeoGebra is a powerful and flexible tool that enables sighted students to solve equations and manipulate mathematical expressions. This program is not accessible for screen readers. To address this, one solution is for braille readers to receive assistance with entering equations and accessing answers in GeoGebra from a sighted person, such as a classmate or an assistant. Entering equations and values into the program does not require advanced mathematical skills. Even if braille readers cannot work independently, collaborating in this way can still be beneficial.
Fortunately, there are other digital tools that are more accessible to braille readers, such as Desmos, AllerCalc, and text-based programming languages like Python.
Desmos
Desmos is a commonly used graphing calculator in many educational settings. Not all features in Desmos are accessible with a screen reader, which can make the program challenging for braille readers. Solving equations graphically is possible but the braille reader only receives the answers verbally through the screen reader. The results are not accessible on a braille display. However, Desmos includes sound cues that represent different characteristics of the graph. This feature can be useful to both braille readers and sighted students.
Example 1
Solve the equation 3x + 3 = 6.
Here is a step-by-step solution using Desmos:
- Write y = 3x + 3 in expression 1
- Press the down arrow
- Write y = 6 in expression 2
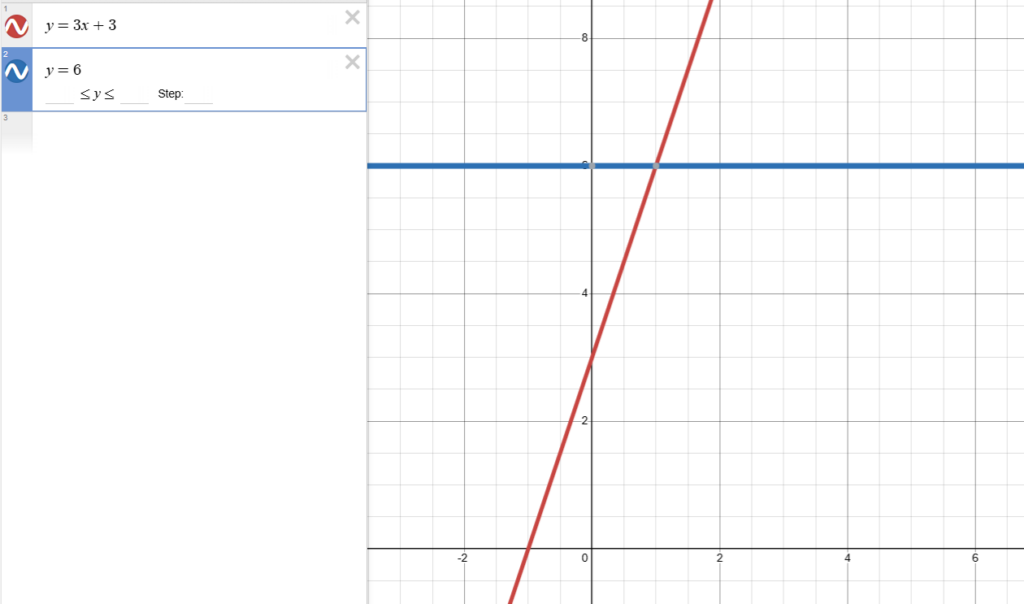
- Press Alt + t
- Press “h” to get a sound representation of the graph in expression 2
- Press Tab to move between and listening to the interesting points of the graph
- Select “intersection with expression 2 at x: 1, y: 6”
- The answer of the equation is x = 1
Example 2
Solve the equation 3x + 5 = 7x ‐ 4.
- Write y = 3x + 5 in expression 1
- Press the down arrow
- Write y = 7x ‐ 4 in expression 2
- Press Alt + t
- Press “h” to get a sound representation of the graph in expression 2
- Press Tab to move between and listening to the interesting points of the graph
- Select “Intersection with expression at…”
- The answer is x = 2.25
AllerCalc
AllerCalc is a fully accessible calculator, developed for visually impaired students. It can find the zeroes of a function, meaning that it can find the solutions to f(x) = 0, within a given interval. In order to solve equations, the student must be able to manipulate the equation such that it ends with = 0.
AllerCalc uses the variable “t”, and not “x”. AllerCalc typically searches for solutions in the interval [‐50; 50], but this can be adapted as follows:
fzeros(“equation” ; “start of interval”; “end of interval”)
Example
Solve the equation x^2 ‐ 4x = 45.
x^2 ‐ 4x = 45
x^2 ‐ 4x ‐ 45 = 0 (set equal to zero)
t^2 ‐ 4*t ‐ 45 (make expression ready for AllerCalc)
fzeros(t^2 ‐ 4 * 4 ‐ 45)
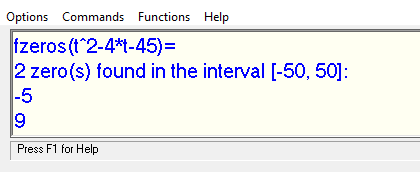
AllerCalc gives the outcomes ‐5 and 9, so the solutions are x = ‐5 and x = 9.
Programming With Python
The SymPy library in Python enables symbolic calculations. Programming in Python (e.g., with Visual Studio Code) can therefore be a good alternative to CAS. As a teacher, you will need to create various programs with designated tasks, incorporating specific lines in the code where the braille reader inputs data. Creating these programs can be demanding and time consuming for the teacher, but once the code is complete, you have the flexibility to vary it extensively.
You can find more information about programming in Python in the instructional guides in computational thinking for ICT professionals and for braille professionals.
Example
Solve the equation (2x + 1)^2 = 14 using the Python code below.
1 import sympy as sp
2 x = sp.symbols("x") # Variable used. Additional variables can be added here.
3 ls = (2*x + 1)**2 # The left side of the equation.
4 rs = 14 # The right side of the equation.
5 L = sp.solveset(ls - rs, x, domain = sp.S.Reals) # Solves the equation ls - rs = 0.
6 print("L = ", L) # The exact solutions.
7 print("L = ", sp.N(L, 5)) # The numerical solutions.
The program gives the solutions to the equation exact and numerical. Symbols to be utilized are specified in line 2, and these can be adjusted or supplemented with additional symbols. Line 3 denotes the left side of the equation, while line 4 represents the right side. The precise solution is recorded in line 6, and if needed, the numerical solution can be added in line 7 (the number in parentheses indicates the number of digits in the solution).
When running the program, the output is:
L = {-1/2 + sqrt(14)/2, -sqrt(14)/2 - 1/2}
L = {-2.3708, 1.3708}